根据麦肯锡2023年6月报告,生成式AI(基于大模型)每年会为全球GDP贡献约2.6至4.4万亿美元,相当于英国2021年GDP总值(3.1万亿美元)。高盛也在2023年4月报告中指出,生成式AI可以为全球GPD贡献7%的增长。此外,早在2017年,普华永道的报告就曾指出,至2030年,AI对中国GDP的贡献可达7万亿美元,相当于中国GDP的26.1%;对美国GDP的贡献约为3.7万亿美元。在普华永道发布该报道时,大模型的概念还未被提出,这说明这波大模型的迅速崛起正好符合了普华对于AI发展的乐观预期。
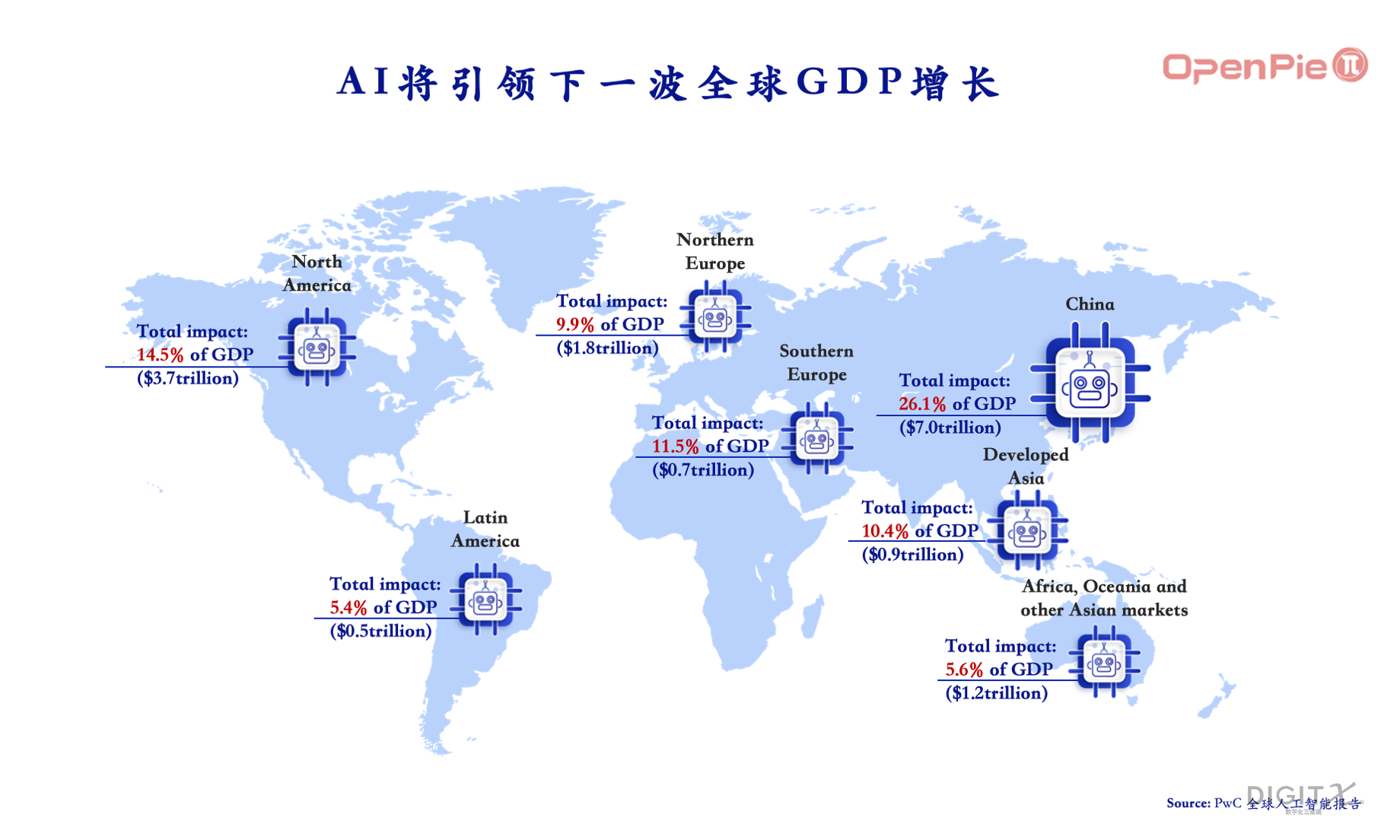
GDP指标原本所衡量的是人类的经济活动规模,然而随着人工智能的日益发展,未来越来越多的经济活动将由AI来推动。从最早的人和AI互动主导经济活动链,到未来越来越多的全AI自主经济活动链。如果不是人在主导经济活动链,那么是“谁”在主导?
答案是数学模型。
从AI-GDP的分析预测来看,人类在使用模型的数量和模型的规模这两个维度上正经历着前所未有的增长。从牛顿提出的万有引力模型,到如今的大模型,到底发生了怎样的量变到质变?深入理解这一技术变革的基础核心,并建立起系统化的方法论,不仅有利于我们在AI竞争中处于全球领先地位,更有利于我们使用AI向善。为此,拓数派提出了“大模型数据计算系统/πDataCS(Computing System)” ,并在Day-1就将自己的使命定位为“数据计算,只为新发现(Data Computing for New Discoveries)”。
接下来,我们从数学化的角度开始,层层展开大模型数据计算系统的设计。我们不仅将深度阐述AI的数学逻辑基础,更将形成一套完整的基础计算系统,以帮助我们在模型的规模和模型的数量这纵深两个维度上不断推进,无限探索数字智能。
数学化
为了深入理解数字智能的基础和边界,我们需要对数学系统进行详细解析。牛顿开天辟地的论文《自然哲学的数学原理》(“NEWTON’S PRINCIPIA : THE MATHEMATICAL PRINCIPLES OF NATURAL PHILOSOPHY”),让我们打开了一道新的理性认识世界的大门。

从17世纪用数学化研究开始,我们用数学建模的方式来观察自然世界,把自然世界的问题映射(Isomorphism)到数学问题,并取得了极大的进展。力学和热学奠定了第一次工业革命,电动力学奠定了电气革命,信息论奠定了信息革命。人们不禁好奇,为什么数学能够这么精准地描述自然,甚至预测未来?莫非这个世界是用数学模型来创立的?当然更主流的观点是,我们用数学语言来描述世界,就好像用汉语或者英语语言来描述世界一样。于此同时,相比于自然语言,数学语言基于严谨的逻辑和算术运算,使得通过电路实现类似于人脑的功能成为可能。
然而,将同样的数学化应用到经济学和社会学时,就没有自然科学那么成功了。直到20世纪50年代的第一次达特茅斯会议开启了人工智能时代,我们以一种全新的数学体系(人工智能的数学)来研究人类和社会行为。那么人工智能的数学和古典数学的质变在哪里呢?(理解这个质变,有利于我们抓住人工智能的最底层逻辑,确保我们研究的底座是世界领先的。)与古典数学化依赖演绎推理不同,AI的数学化更多地依赖计算。为了帮助读者更好地理解这一转变,让我们先结合实际例子帮助形成直观感受。
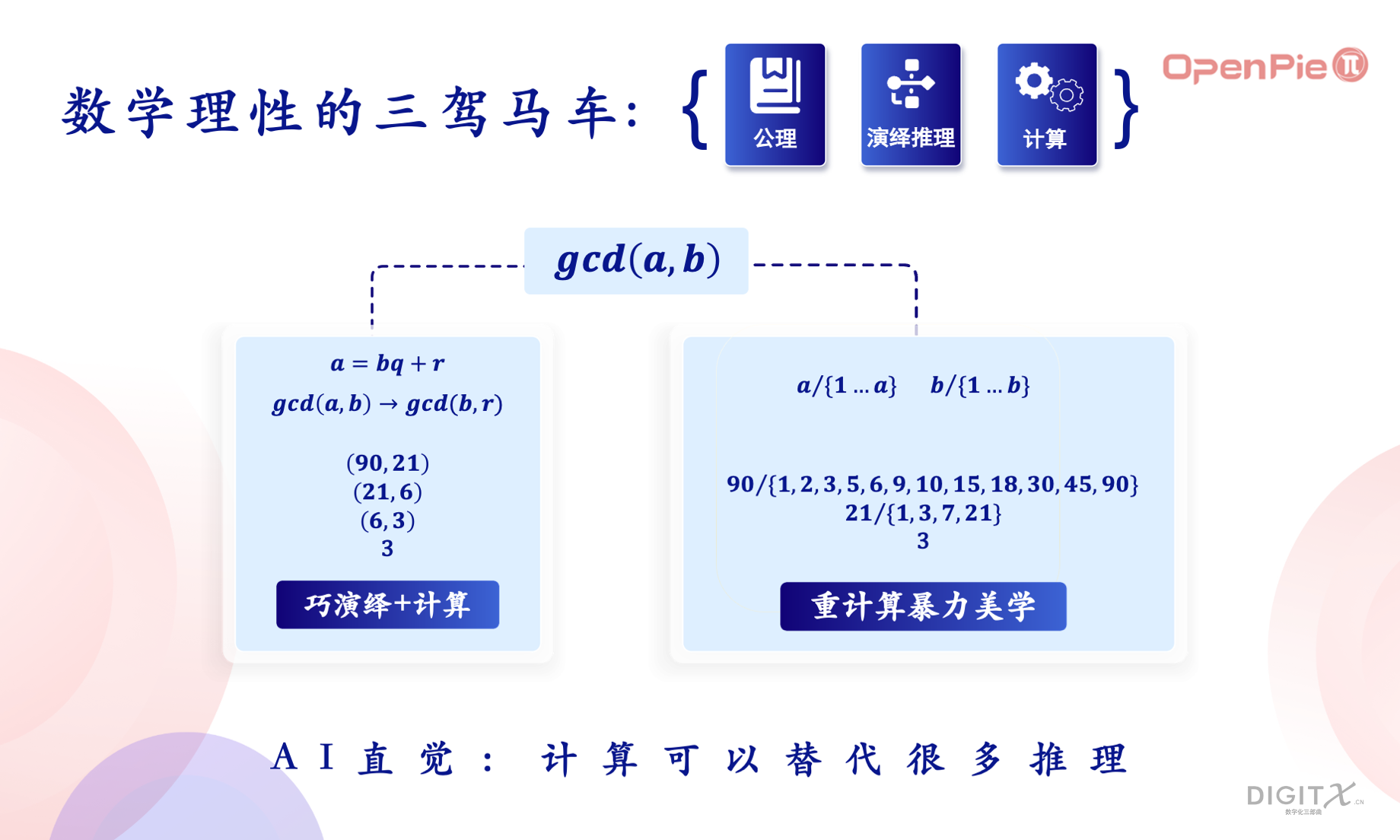
Source:《计算进化史》
数学系统的核心包括公理、演绎推理和计算三个要素。我们先来观察一下演绎推理和计算在求解最大公约数问题时的不同侧重点。如上图所示,左边的方法是辗转相除法,它的基础是一个巧妙的推理:a和b的最大公约数等价于b和它们的余数的最大公约数。如此辗转,当余数为0时,b即为最大公约数。而右边的方法则采用直接暴力求解的方式,逐个除以1到a的每个数,找出能整除a的数作为其约数,并对b进行类似操作。然后比较a和b的约数集合,找出最大公约数。如果是考试,使用左边的方法可能让你更快地得到结果,但是这个方法过于巧妙,读者很难自己构建这样的算法。相反,右边的方法非常容易实现,尽管它需要更多的计算量,但计算机在进行暴力计算方面非常擅长。
计算
通过前面的例子,我们形成了一个数据计算系统的直觉:用计算可以替代更多的演绎推理。那么,我们如何设计一个系统,让计算可以替代更多的推理,从而使得AI能够快速而广泛地铺开呢?拓数派的数据计算系统的核心观点是从公理化数学的视角切换到数据计算的视角。
古典数学建立在公理化体系之上,公理化数学在“数字化三部曲”中的第二部曲《Greenplum:从大数据战略到实现》的第一章有详细讨论。欧几里得的几何学最初从五个公理出发,加上古典逻辑推理规则(包括同一律、排中律、无矛盾、蕴含的单调性和蕴含的幂等性、合取的交换律以及德·摩根对偶律),奠定了整个欧几里得几何体系。这个体系不仅一致,而且完备。因此古希腊人把推理运用到了极致。后来人们发现,第五公理选择不唯一,产生了非欧几何学,但它仍然与欧几里得几何学相兼容。
为此,哥廷根的希尔伯特希望对数学引入逻辑公理和算术公理,为重新奠定数数学的基础。他在1927年出版了《数学基础》(Foundations of Mathematics),创造了形式化数学(Formalism*)。然而,希尔伯特的著作至今没有被翻译成英文或者汉语。希尔伯特希望提出的系统是一致的,完备的,可判定的。但是哥德尔证明了这个系统是不完备的,也就是说,存在一些数学公式无法从算术公理和逻辑公理中推导出来。另外,这个系统的算术公理(与集合论公理等价)的选择上也不唯一,而且不同选择间不像几何第五公理的选择那样可以兼容(参考《数学简史:确定性的消失》第13章)。
然而,希尔伯特的形式化理论最大的影响就是将计算提升到了重要的地位。希尔伯特希望他的系统是可判定的,即对于给定的任何一个数学公式,能够从公理出发,按照推导规则来操作数学符号,以判定该公式是否成立。希尔伯特(和之前的莱布尼兹)提出了可判定性问题,本质上是希望把数学推理通过计算实现机器化。为了证明可判定性问题无解,邱奇引出了计算的λ(lambda)演算定义,而图灵给出了图灵机定义,后来证明两者是等价的,图灵后来也成为了邱奇的研究生。我们在探讨理论数据计算系统的时候,是基于λ演算的,因为它的规则非常简单。在讨论数据计算系统实现的时候,是基于图灵机的,因为现代程序是基于图灵机实现的。拓数派的创始团队合伙企业叫“哥廷根”,旨在继承和发扬德国哥廷根大学在计算领域的出色起始工作。
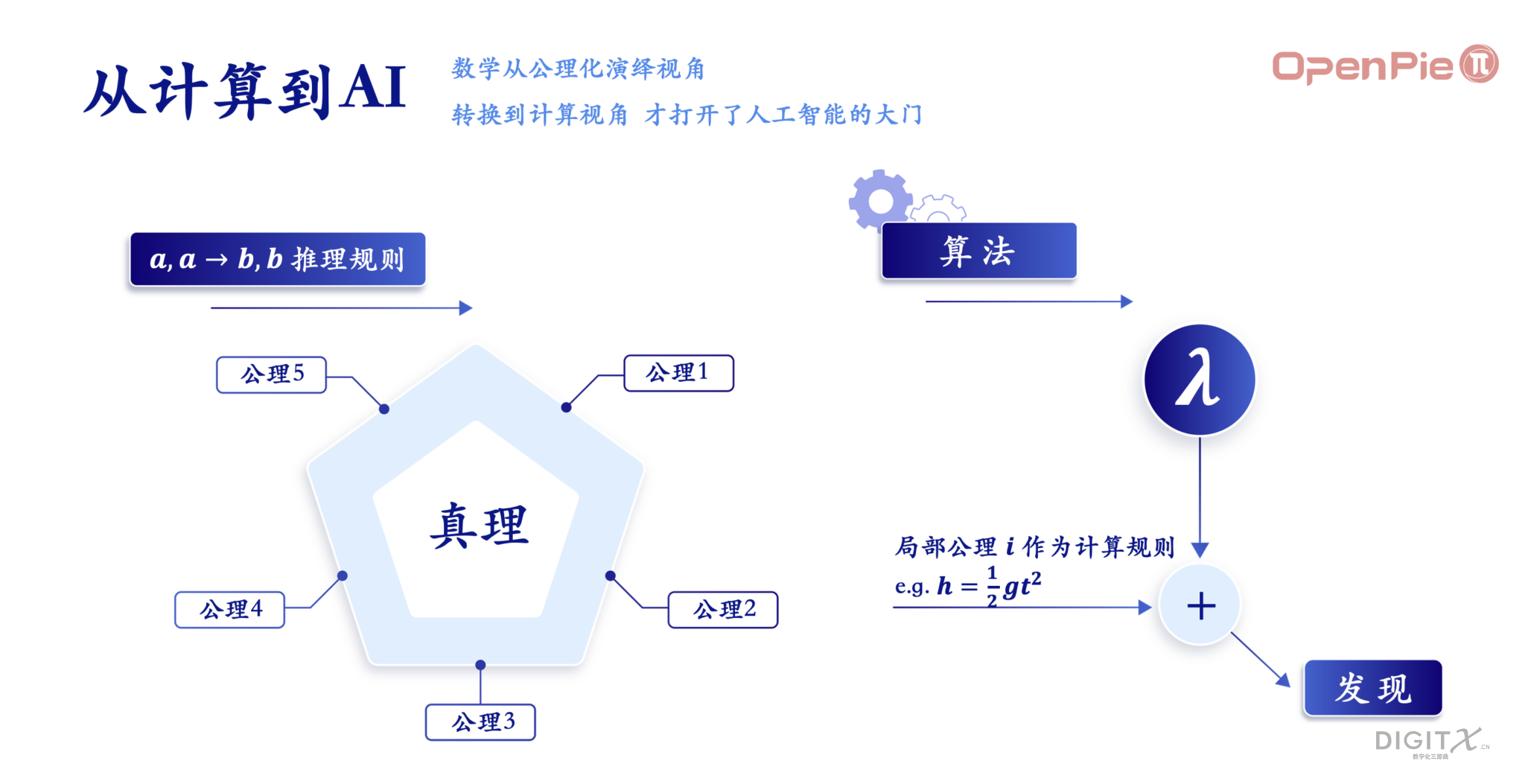
鉴于基于逻辑公理和算术公理的体系非常庞大且不一致,同时公理的选择也不唯一,拓数派认为我们可以从计算规则出发,借助λ演算的原生规则,在待解决的实际问题中,引入和领域相关的计算规则。此外,基于λ演算的系统设计,可以在计算机上通过逻辑和算术门电路实现。例如,在自由落体运动的过程中,我们可以引入h=1/2 gt^2 这样的计算规则作为局部公理,来探索自由落体问题中的发现。那么问题来了,我们应该如何去寻找大自然母亲的计算规则并将其引入到计算系统中?答案是通过模型和数据计算。
数据计算
在寻找局部领域的计算规则时,我们可以构建一个初始模型(Raw Model,未训练的模型),然后通过计算,使用与该模型对应的观察到的数据进行训练。训练完的模型就形成了一个计算规则,并引入到我们的计算系统,拓数派把这种方法定义为“数据计算”。
为了帮助读者理解,我们以自由落体计算规则的形成为例。我们采用线性回归方法来构建初始模型,假设我们引入两个不同变量(物体的质量和下落时间),我们的初始模型如下图所示。为了训练这样的初始模型,我们需要收集数据,假设我们收集了6组不同的数据,我们就可以把初始模型和数据输入到拓数派的数据计算系统中,拓数派的数据计算系统输出训练好的模型 h=5t^2,而这个训练好的模型就可以引入到拓数派的数据计算系统,成为自由落体类相关问题的局部计算规则(类似公理)。
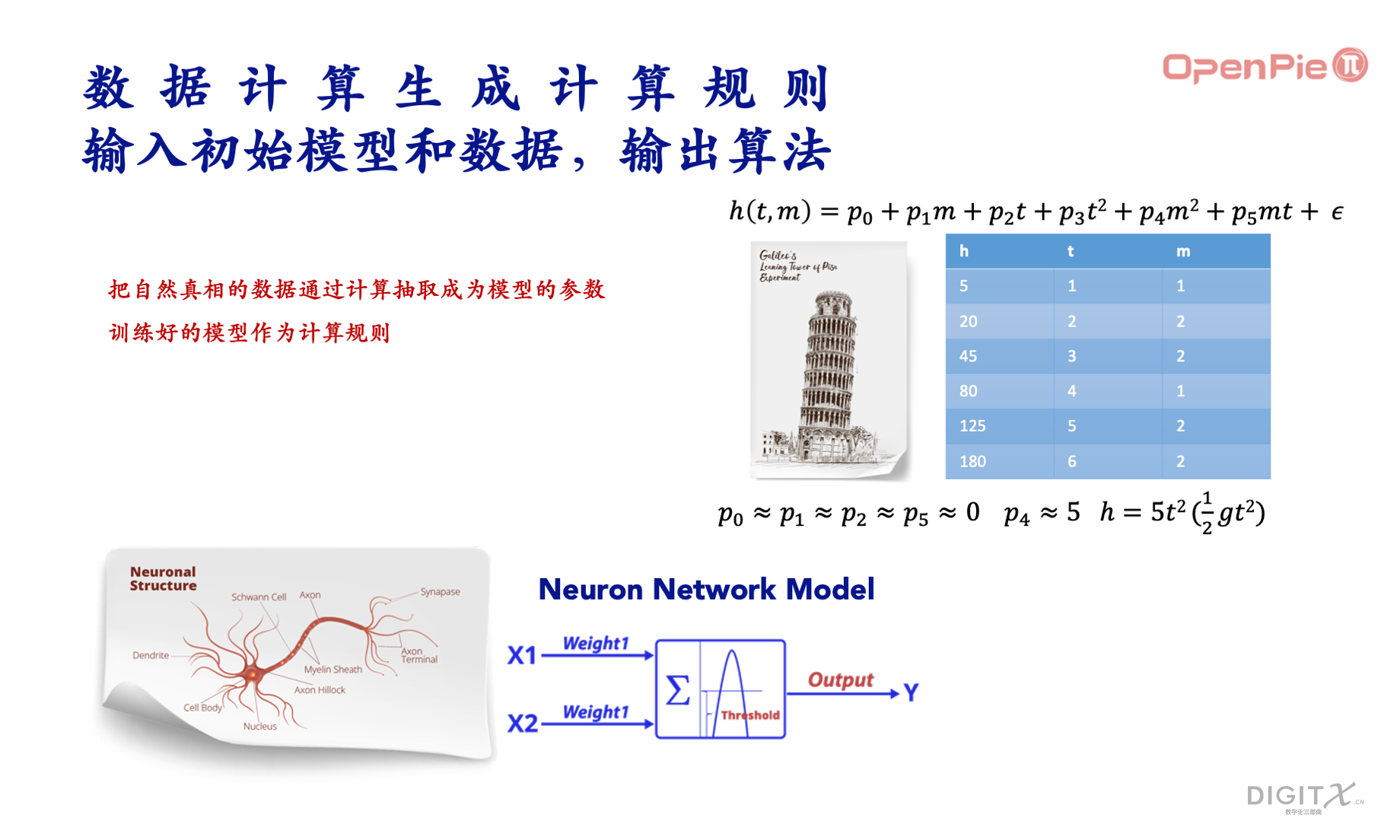
这个初始模型的构建,从简单的线性回归,到现在的神经网络,构建方法越来越多,模型越来越大,这是这次大模型从量变到质变的原因。然而,大家需要牢记的是,通过数据计算形成的这些计算规则类似于公理,它们并非通过严格的逻辑推导得出。因此,在特定领域中使用这些计算规则时,我们必须保持警惕,以确保其有效性。
数据计算系统
现在,我们可以通过数据计算来生成新的局部计算规则,并将其引入到我们的数据计算系统中。拓数派的数据计算系统可以被定义为:通过对初始模型和数据进行训练,形成新的计算规则。这些计算规则可以被视为局部公理,并重新插入到数据计算系统中,从而进行迭代,形成新的数据计算系统。
这个时候,一个自然的宏大目标是对世界万物和运动进行数字化,形成相应的数据,再通过初始模型来训练形成计算规则,并将其补充到拓数派的数据计算系统。随着数据量的增加,另外一个宏大目标必然是支持越来越大的初始模型,形成大模型数据计算系统。基于这一背景,一个自然的问题是:大模型数据计算系统的终极目标是什么?

我们已经知道,通过基础模型可以适配到各个领域模型,从而派生出新的模型。如果我们将这些领域模型记作第一层Layer1,那么基础模型则是第二层Layer2。与此同时,行业在Layer2上也在不断产生新的基础模型,例如GPT,BERT,DALLE,MidJourney。我们自然会问,是否存在Layer3的模型,可以帮助调度、适配和解释Layer2的模型。对这个模型的探索可以持续下去,无限逼近终极模型(Master Model),从而形成一个无限游戏。流行文学一直在讨论终极模型和人类智能的关系,对于理性的讨论,可以参考“数字化三部曲”的第二部曲《Greenplum:从大数据战略到实现》的“AI和人”的讨论章节。
大模型数据计算系统
数据计算系统的纵向探索是一个无穷尽逼近终极模型的过程。数据计算系统的横向讨论则是创建更大的模型,形成大模型数据计算系统。在“数字化三部曲”的第二部曲《Greenplum:从大数据战略到实现》中我们已经讨论过,更多的模型,更多的参数,更多的数据,一般来说都会训练出更好的结果,也就是形成的新的计算规则更加准确。

Michele Banko and Eric Brill, Scaling to Very Very Large Corpora for Natural Language Disambiguation
为了支撑更大的模型,我们数据计算系统的理论在物理实现上,必然需要选择当代最先进的计算平台。计算平台从大型机、PC机到如今的云平台经历了三代大的变更。云平台代表了目前最大的计算能力、存储能力和水平扩展能力。虽然云计算已经存在了近20年,但当代数据工具和平台大部分还是针对PC架构设计的,它们在云上处于被向下兼容模式,属于逆大模型技术。幸运的是,拓数派团队作为原生理念提出的重要力量,在云原生方面提供了重要的推动力。因此,拓数派的大模型数据计算系统必须Day-1针对云原生重新设计。我们将在下一篇《大模型数据计算系统–实现》中详细展开讨论。
附录
*作者认为翻译成正式化数学更加准确
[…] 冯雷|数字内核「向外…
[…] 为了支撑更大的模型,…
[…] 在《大模型数据计算系…
[…] 【上接:…
[…] 「上接:…
“大模型数据计算系统——理论”的一个回复