上一节谈到了人类的经验知识是分层次的。总结一下苹果落地的两个层次。第一类层次,因为我们看到了苹果总是往下落地,没有往上飞过,所以我们认为苹果是落地的,第二类层次,我们建立牛顿古典力学模型,因为物体受力要朝受力方向加速前进,所以苹果脱离树枝以后,受到地心引力要朝地表方向前进。在这一个层面,古典力学的很多模型的选择(例如,万有引力距离平方成反比;再例如不同参考系时间流逝是一样的。)其实也是经验的。人类把知识一层层往上逻辑化到认知边界,依赖几个感性的假设,建立了一个认知体系。
很多伟人倒过来看:能否依赖于几个基本的公理假设(感性选择)来建立整套认知体系?从欧几里得到希尔伯特,哲学、数学和物理学科的学霸们分别对几何知识和代数知识进行逻辑化。而这个过程中,人类开始构想,能否让机器从几个公理和规则通过计算推演,列出所有人类知识?这直接导致了以图灵机为代表的机器智能的产生。图灵在他的经典论文《论可计算数》中构造了一个机器(后人称为图灵机),来模仿人类数学工作者。物理计算机的发明在后面的章节上会讨论,但学术界普遍认为物理计算机的发明是受到图灵机的启发。冯·诺依曼等人在发明物理计算机后,给原本清贫的数学工作人员创造了高薪的编程岗位。前面在AI小节中谈到,今天的AI技术建立在计算机之上。理论上讲,AI学科只是图灵机系统的一个模型化算法子集。在这个子集里面讨论AI智能和人的关系必然是不完整的。所以在讨论AI和人的关系上,我们需要再往上追溯到公理化数学的过程。正是这个过程,邱奇、图灵和哥德尔等人对于机器和人的探讨远远深过今天大众传媒对这个话题的讨论。
第一个建立公理化的逻辑系统是欧几里得的《几何原本》。如果追溯到数学的源头,欧几里得可能是个不得不提的人。他的著作《几何原本》对于人类影响非常深刻,据说《几何原本》在西方的发行量仅次于《圣经》。欧几里得的整个几何体系建立在5条公理之上。为了避免读者再去翻初中几何课本,5条公理如下:
- 过相异两点,能作且只能作一直线(直线公理)。
- 线段(有限直线)可以任意地延长。
- 以任一点为圆心、任意长为半径,可作一圆(圆公理)。
- 凡是直角都相等(角公理)。
- 两直线被第三条直线所截,如果同侧两内角和小于两个直角, 则两直线作会在该侧相交。(平行公理)
其中第五条公理可以用另一种方式表述为:在一平面内,过直线外一点,可作且只可作一直线跟此直线平行。
欧几里得平面几何(欧氏几何)的所有定理可以最终追溯到这五个公理,所以这五个公理构成了欧氏几何的边界。作者初二的时候理解边界也有点困难,到后来也就放弃追问欧几里得为何如此定义此五公理。后来我才知道,很多学霸都不喜欢欧几里得看上去像“主观臆断”定义的第五公理。其中有个俄罗斯人叫罗巴切夫斯基(后面简称罗氏,虽然他不姓罗),他认为第五公理应该可以通过前面四个公理推导出来。为了推导这个公理,罗氏使用了反证法。在反证法中的第一步,他假设 “过直线外一点有两条平行线”,然后试图通过这个反证假设来结合前面4条公理推导出逻辑矛盾。如果推导出矛盾,那么假设错误。但是,罗氏基于他的假设并没有推导出任何矛盾,反而推导出一个和欧氏几何完全平行的几何体系——罗氏几何体系,也就是双曲几何。为帮主读者视觉化罗氏双曲几何,图一为一三角形于一双曲抛物面上,另外右下方有两条在欧氏几何中应平行的分流线。
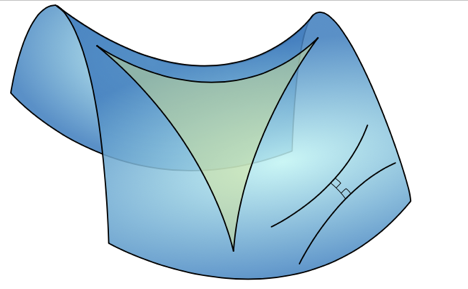
罗氏几何体系完全不同于欧式几何,开创了非欧几何的先河。一方面,这意味着欧几里得并不是随意选择了他的第五公理,他必须要选择第五公理才能建立起来他的欧氏几何。另一方面,这也意味着罗氏可能惹上了和哥白尼一样的大麻烦。哥白尼说地球不是宇宙中心,因为违反宗教教义被活活烧死。罗氏理论标志着两个几何世界的出现:一个是欧氏几何描述的方方正正的世界,另外一个是罗氏几何描述的弯弯曲曲的世界。由于颠覆了当时大众广为认知的体系,罗氏的理论因此受到很多非议,他个人也遭受了很多不公正待遇。这时,罗氏向另外一位学霸、有数学王子之称的高斯求助,希望高斯能够公开支持他的理论。高斯虽然提供了很多力所能及的帮助,但是最终没有公开站出来支持多个几何体系的存在。尽管高斯自己也感觉到第五公理的选择不是唯一的,但是他深知愚昧势力对于新事物的恐惧。(这里插一句,如果读者像哥白尼、罗氏、麦克斯韦等人一样聪明,在认知边界上突破,记得把你的理论在抽屉里放一段时间。当然如果害怕自己的理论被别人先发表,记得在发表观点的时候要承担被吃瓜群众拍砖的风险。其实某种程度上群众今天对于AI的恐惧也只是历史重现。)
罗氏的晚年在不幸中度过,他的理论一直没有公开得到支持。直到1868年,意大利数学家贝尔特拉米发表了一篇著名论文《非欧几何解释的尝试》,证明非欧几何可以在欧几里得空间的曲面(例如拟球曲, pseudosphere)上实现。也就是说,非欧几何命题可以“翻译”成相应的欧几里得几何命题,如果欧几里得几何没有矛盾,非欧几何也就自然没有矛盾。直到这时,长期无人问津的非欧几何才开始获得学术界的普遍注意和深入研究,罗巴切夫斯基的独创性研究也就由此得到学术界的高度评价和一致赞美,他本人则被人们赞誉为“几何学中的哥白尼”1。
自贝尔特拉米解除了宗教势力对于非欧几里得几何(非欧几何)的束缚以后,来自德国哥廷根大学的高斯和黎曼对非欧几何进行了大刀阔斧的拓展。黎曼对于欧式几何的第五公理做了另外一个相反的假定:过直线外一点,不能做直线和已知直线不相交。由此产生了非欧几何的另一个分支——椭圆几何。高斯有数学王子之称,黎曼应该是高斯的继承人。关于高斯和黎曼在非欧几何的突破性进展,可以参考陈省身1987年在台大的演讲《什么是几何学》²。嘉兴籍数学家陈省身是公认的20世纪微分几何学家,曾在加州伯克利等名校任教授。我们这里不是为讨论几何而讨论几何著作。
总结来说,对欧几里得第五公理作不同假设,最终衍生出三种逻辑自恰的几何学:罗氏几何、欧式几何和黎曼几何。三种几何中,垂直于同一线段的两条直线如下图所示:左:罗氏几何(双曲几何)、 中:欧式几何、和 右:黎曼几何(椭圆几何).
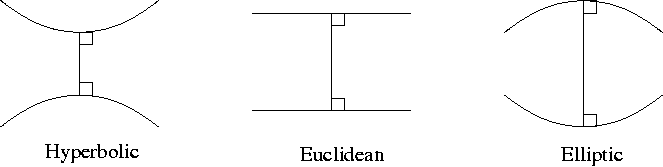
读者读到这里可能着急起来。计算机(人工智能)和几何有啥关系?因为非欧几何的公里化体系的讨论,激发了自然数算数体系公理化的类似讨论,从而导致了算法的图灵机的定义。这里需要首先引出哥廷根大学的另外一位学霸:希尔伯特。 在高斯和黎曼之后,非欧几何在哥廷根大学盛行,影响了不少数学家。哥廷根大学迎来了希尔伯特,希尔伯特提出了公理化几何体系并出版了《几何基础》。 整个体系从一组公理出发,层层推导。希尔伯特的公理化方式也表示数学方式开始转移到现代的公理系统。公理系统可以摆脱现实世界,就像非欧几何的不同第五公理可以创造出不同生活直觉的几何世界。如果说几何学是探讨几何元素的关系,那么如点、直线、平面等可以用桌子、椅子等物体所取代3。更为重要的是在希尔伯特的概念里面,一个从公理化构造出来的完整的数学系统应该具有以下特性4:
- 独立性:系统里面的各个公理相互独立,任何一个公理都不能从其他公理推导出来。例如欧几里得的第五公理并不能从其他四个公理推导出来。
- 一致性:从公理出发,不能推导出两个互相矛盾的定理。假设B是A的反命题,我们不能从公理系统中同时推导出A和B成立
- 完备性:从公理出发,可以推导出所有真命题。假设B和A是反命题,但是从公理系统不能证明A或者B,那么系统是不完备的。因为A和它的反命题都可能是对的,不完备的系统像知识世界存在黑洞一样,让人不安。
- 可判定性(Entscheidungsproblem):给定一个数学命题,是否可以从公理出发,通过有限计算步骤,来判定这个命题的可证明性。这个可以列举的计算步骤就是现在意义上的算法(Algorithm)。
完备性和可判定性可能有点让人混淆。如果一个系统是不完备的,那么存在命题不可被证明。可判断性说的是否能找到一个步骤,计算出一个命题能否被证明。
希尔伯特的伟大之处就是在于把公理化系统的思考方法影响到代数体系。在1900年8月的国际数学家大会上,希尔伯特将可判定性问题列为当时数学面临的23个问题中的第10个问题。他的第10个问题向数学家同僚挑战:“是否可以推导出一个过程(算法),通过有限步骤判定不定方程(也叫丢番图方程)是否存在有整数解的命题?”希尔伯特的座右铭是:“我们必须知道;我们必将知道。”在他眼里,不定方程无论是否有解,都应该存在一个判定过程,判定它是否可以被证明。例如费马方程:![]() 作为一种特定形式的不定方程,在数学家们试图证明命题“费马方程在自然数 n > 2 的情况下不存在整数解”之前,希望有个判定过程(算法)来判定它是否可以被证明。
作为一种特定形式的不定方程,在数学家们试图证明命题“费马方程在自然数 n > 2 的情况下不存在整数解”之前,希望有个判定过程(算法)来判定它是否可以被证明。
事实上费马定理的证明花费了数学家300年的努力,幸运的是它是可证明的。至此,大家长嘘一口气,不然300年努力就白花了。从费马定理证明史这个例子上可以看到,代数命题通用判定过程(算法)的意义重大。要讨论通用的可判定性,首先需要清晰地定义什么是算法。为此,邱奇和图灵分别提出了不同构造和定义。图灵构造了图灵机,然后算法就定义在图灵机的操作之上。下一节将讨论图灵如何构造图灵机,但是很遗憾图灵也证明了基于自然数算术的公理化体系的通用判断过程并不存在。
- 参考 https://zh.wikipedia.org/wiki/罗氏几何
- 陈省身 ;张奠宙,王善平《陈省身文集》p287 华东师范大学出版社 2002年
- 参考《几何学公理化》,https://zh.wikipedia.org/wiki/大卫·希尔伯特
- 我们这里没有采用严格的数理逻辑语言,部分内容参考Charles Petzold著,杨卫东等译《图灵的秘密》,第三章。
《AI和人》系列快速链接
作者介绍
冯雷(Ray Feng)是Pivotal中国公司MD兼研发中心总经理。Pivotal中国成立至今,冯雷主持了近十亿人民币投资的中国运营和研发体系。作为Pivotal全球产品关键领导人,冯雷为Pivotal公司的数字化理念建立及其对应的Cloud Foundry和Greenplum产品提供战略输入。冯雷于2010年从美国硅谷归国,在美国500强公司EMC旗下组建了Pivotal中国。在归国之前,冯雷居住在美国加州硅谷,在500强企业甲骨文(Oracle)总部从事云计算产品研发。作为云计算最早一批从业人员,冯雷帮助甲骨文云计算资源调度领域成为意见领袖。学术方面,冯雷以浙江省队物理奥林匹克银牌进入北京大学。冯雷在北大实验班(现在的元培项目)接受计算机科学和数学在内的基础学科熏陶,并获得物理学和经济学双学士。冯雷研究生就读于美国匹兹堡市的卡内基梅隆大学并获得硕士学位,在校期间在机器人学院(Robostics Institue)从事教育机器人项目助研。冯雷持有两项美国云计算专利,并著有云计算、大数据和AI的三部曲著作.
[如需转载请注明本文URL] [https://digitx.cn/2019/03/25/ai和人_第2节_公理化的逻辑系统/
“《AI和人》第2节:公理化的逻辑系统”的3个回复