《AI和人》第4节：认知边界上的考量

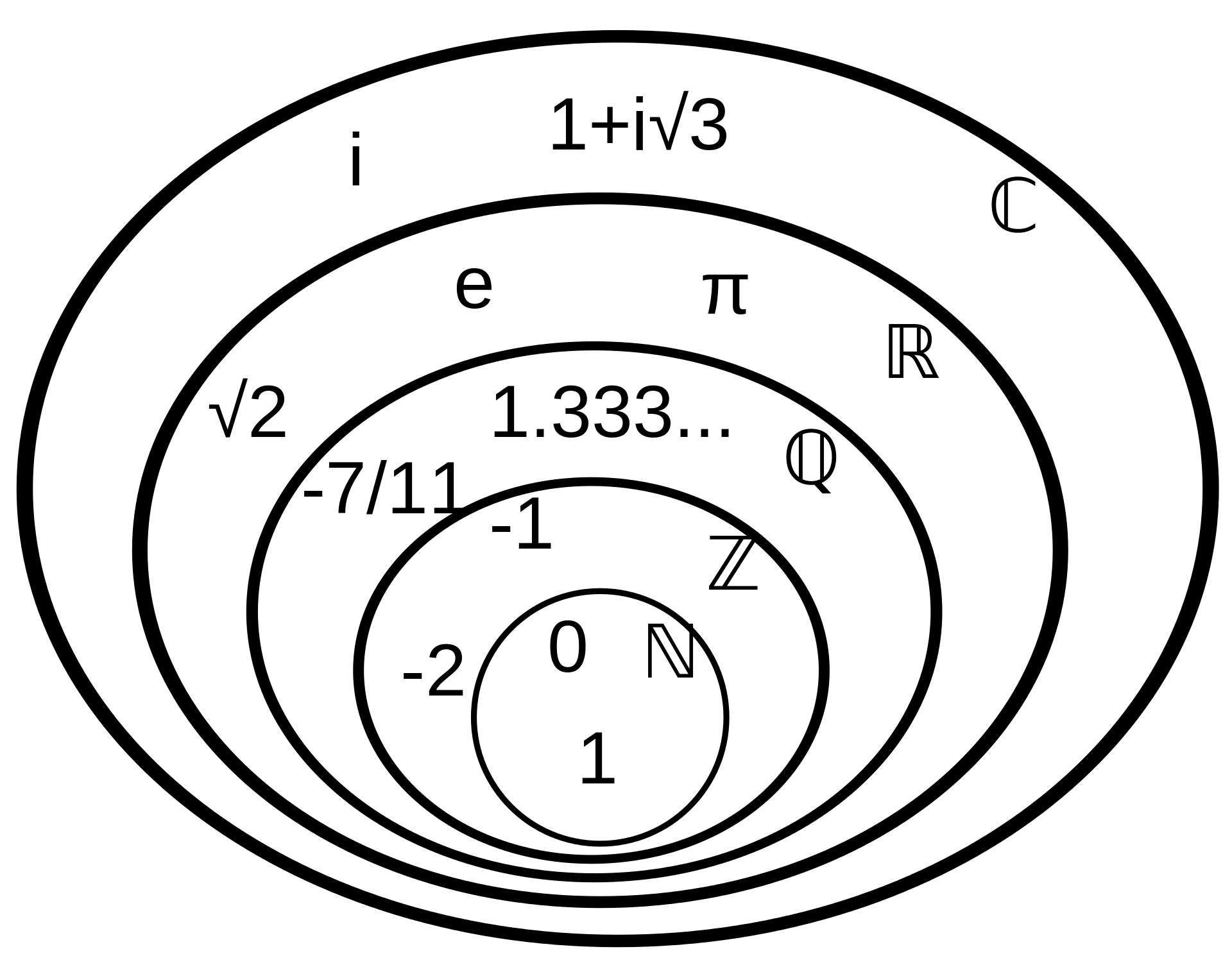
人工智能是否会取代人类这个问题，实际上涉及对于认知的无穷边界的考量：图灵机能表达的带有人工智能模型的可计算数（程序）无穷大，人的思考过程也无穷大，哪个无穷大更大？面对这个问题，大部分人的反应：“两个无穷大还有大小？”所以，这里有必要重新理解一下数。数有两个让人最头疼的问题：无穷问题和无理问题。据说知名的数学家、集合论的创始人康托尔(Cantor)就因为沉溺于数的无穷问题而得了躁狂型抑郁症。作者无意将这种痛苦加载在普通人头上，但是对于思考AI是否要取代人的读者，这个是绕不过去的坎。

自然数集、有理数集合和无理数集合在有限情况下非常容易理解，但是在无限的情况下很多属性会发生变化。 我们看下面两个集合（N为自然数）：

• 自然数集合A {1，2，3，4，…，2N}
• 偶数集合B {2，4，，…， 2N}

在N是个有限的数下，集合A的元素的元素数（叫做基）是集合B的基的两倍。但是当N无穷大的时候，两个集合的势（无限集合的基）就相等了。为什么呢？偶数集拿出一个2，自然数集合拿出1，偶数集拿出4，自然数集拿出2，这样无穷下去。可以用无穷自然数集1对1数的无穷集合叫做“可数”。一个无穷集合如果可数，那么它们的基就是和自然数集A相等的。读者可以尝试证明一下无穷有理数集合也是可数的，只要把集合元素顺序的写法写得可数。具体做法就是把分子分母之和等于1，2，3，4的自然数一一列举如下：

• 有理数集合C {1/1，1/2，2/1，1/3，2/2，3/1…}

读者可能兴致勃勃地把这个可数数的证明推广到实数集，但是康托儿用对角论证法证明了实数集合是不可数的。因为康托尔的证明激发了图灵只讨论[0,1]区间的二进制形式的数，而使用二进制对实际计算机的发明产生极大的帮助。这里简单介绍一下这个证明方法，具体证明方法可以参考维基百科¹。假设我们数完了所有的[0,1]之间的实数r₁ , r₂ ，举个”象征性”的排列例子如下（来自维基百科）：

r₁ = 0 . 5 1 0 5 1 1 0 …

r₂ = 0 . 4 1 3 2 0 4 3 …

r₃ = 0 . 8 2 4 5 0 2 6 …

r₄ = 0 . 2 3 3 0 1 2 6 …

r₅ = 0 . 4 1 0 7 2 4 6 …

r₆ = 0 . 9 9 3 7 8 3 8 …

r₇ = 0 . 0 1 0 5 1 3 5 …

记得我们现在把所有无理数数完了。我们创造一个新的超越数²，它的第k位取自于上面数字r_k的小数点后的第k个位并加1，如果遇到9变成0。所以这个新数就是0.6251346…它和上述的数都不一样，所以它不在这个可数数列表，因此实数集是不可数的。这个证明带来另外一个非常有意思的结论：同样是无穷，实数集合的无穷要比自然数集合的无穷要更大。如果把自然数集合的势记为aleph-0(康托尔把它叫做超限数并用俄文字母标记为  )，康托尔想去计算实数集的势，为此他引入了[0,1]区间的二进制形式的数和集合论。他尝试用小数点后无限位二进制数的0和1的交替的记法去对应实数里面的元素。为帮助读者理解，列举几个数如下：

0.0000000…

0.1000000…

0.0100000…

0.1100000…

0.0010000…

0.1010000…

0.0110000…

0.1110000…

如果我们把1当做✓一样的标记，学过子集的读者肯定觉得这个标记和列举含3个元素{0, 1，2}集合的所有子集的记法很相似：

含元素0	含元素1	含元素2	…	对应子集
				{}
✓(1)				{0}
	✓(1)			{1}
✓(1)	✓(1)			{0,1}
		✓(1)		{2}
✓(1)		✓(1)		{0,2}
	✓(1)	✓(1)		{1,2}
✓(1)	✓(1)	✓(1)		{0,1,2}
				…

将这个二进制小数列表无穷列举下去，那么对应的子集表也可以无穷列举下去³。这些二进制形式的小数对应了所有[0,1]区间的实数⁴，而表格第五列中子集的列表也等同于无穷自然集的子集。因为一个含有N个元素(基为N)的集合的子集数目为，无穷自然数子集的数目就是 ，这个数也就是实数集合的势。康托尔猜测 就是下一个超限数aleph1（  ），中间不存在其它超限数，也叫连续统假设。这是希尔伯特提出23个问题中的第一个问题⁵。

因为康托尔的工作，我们知道了实数集与可数数集同样是无穷大，但是实数集要更大。图灵发明了图灵机和定义在其上的可计算数，所以图灵自然要考虑：“可计算数对应了可数数还是整个实数集？”很遗憾的是，图灵证明了可计算数虽然包含了无理数中的代数数（例如 这样的代数方程的解）和部分超越数（例如 π 和 e ），但是它是可数的。可数数的势aleph0(  ）远小于实数集合的势  。而世界万物都是数，而且大部分数都是实数，实数中的大部分超越数都无法用图灵机表示。这意味着什么？第一个选择是我们拒绝承认不可计算的实数的存在，这就等同于我们构造了不存在的数；第二个选择是我们承认它们的存在，图灵机无法表达一个随机生成的无理数。那么人脑是否有个思考过程能否对应一个无限、无理的数？而图灵和邱奇恰恰就是这么认为——人脑也不行，这就是他们提出了的邱奇图灵论题。这个论题可以简单地表述为：“凡是人类能够执行的算法，图灵机也可以。”⁶用其等价的逆反命题来说是：“如果算法过程是图灵机不能解的，人类也不能解。”到这里，读者可能这里有以清晰地知道，这个是论题，它并不能被证明。人工智能是否能够取代人，本质上也依赖于这个论题是否正确。在作者眼里，这个论题就像几何的五个公理或者物理学里面的能量守恒定律一样，是我们公理化的认知边界。

到这里，读者已经看到图灵机上能表达的可计算数是无穷的，但是有个更大的实数无穷是图灵机无法表达。这两个极限的差别表现出图灵机的解决问题的范畴是有局限的。举个例子来说，我们不能发明一个程序检查另外一个程序的错误⁷。一个错误的程序会使图灵机就会进入失控状态，计算过程会进入到一个表格里面不存在的状态（m-config）。回到希尔伯特可判定性的讨论，图灵试图构造一个图灵机，从希尔伯特的《数学原理》中的几个公理和规则出发，让图灵机列举出所有可证明的公式。但是图灵证明了这样的图灵机不存在。根据邱奇图灵论题，人类数学工作者也找不到一个思考过程判断一个公式的可证明性。

图灵接下来讨论了一系列人和机器智能的问题。在1950年的Mind杂志上，图灵就人工智能这个话题发表了另外一篇论文“Computing Machinery and Intelligence”⁸。在论文中，他提出了“机器能够思考吗？”这个问题。他认为思考和机器(读者可以认为AI)的定义过于模糊，为此他给出了知名的图灵测试来回答这个问题。在图灵测试中，被测试者（人）在一个黑暗的屋子里面与一台机器和一个人进行对话（那个年代以文本方式，现在则可以升级到语音方式），若被测试者无法区分对话的是人还是机器，则可以称机器通过了图灵测试。这也是电影《机械姬》的一个故事情节基础⁹。

我们如何看待邱奇图灵论题决定了我们怎么看待人和AI之间的关系。为帮助读者理解邱奇图灵论题，作者这里尝试用通俗易懂的语言来表述。图灵机在某个状态下观察一个符号，然后状态切换到下一个状态，这个行为和我们人类数学工作者几乎一样。差别在于，邱奇图灵认为机器的状态是有限的，类似于我们构建的表1-1的行状态是有限的¹⁰。图灵认为，如果人脑允许有无限的状态，必然因为有些状态无限接近而造成混乱。但是作者认为“人的思想可以支持一个无穷状态”，因为我们对人的意识理解得并不清楚，证明数学不完备性的数学家哥德尔也表示了类似的观点¹¹。不管如何，机器智能或者人工智能的产生，极大地解放了人类在可计算数范围内的求解问题速度。机器智能的诞生似乎加速了人类对于数字世界中未知领域的探索。只是，我们对于新生事物的直觉反应总是恐惧，对机器智能的兴起也一样的反应。图灵认为人类在上个世纪末不再会抵触和反对机器思考。但是到了今天，我们还是因为不了解或无法掌控机器智能而产生恐惧或不安，过度的恐惧和不安又有可能限制我们充分利用机器智能的长处，进而错过对于机器智能以外的世界的探索。

我们今天感受到的数字世界，存在一定的公理和论题上的边界。在这个边界里面也有黑洞，原因是不完备性；我们也没有一条快速路径来鉴别黑洞，是因为不可判定性。但是如果你和作者一样认为人的意识格局比图灵机格局具有无限性，那么应该持续地去拓展这个边界。在这个边界拓展或者重构的时候有些黑洞或许会消失，或许可以找到一条路径鉴别黑洞。就像希尔伯特说的：“我们必须知道；我们必将知道。”

---

 

1. 完整证明方法参考https://zh.wikipedia.org/zh-cn/对角论证法
2. 无理数分为代数无理数和超越数。超越数的代表是e和π。
3. 注意这是无穷环境, 这个例子形式只能帮助逻辑上推理而不是准确的表述形式
4. 如果考虑整体实数，负数可以通过绝对值对应到正数，大于1的正数可以通过倒数对应到[0,1]。
5. 由于不完备性的影响,已经在数学上证实了该假设不能被证明为真或假。
6. 参考https://zh.wikipedia.org/wiki/邱奇－图灵论题
7. 学术语言说是不能发明一个程序检查一个程序的停机问题
8. https://en.wikipedia.org/wiki/Computing_Machinery_and_Intelligence
9. 电影《机械姬》认为即使被测试者发现对方是机器也无法阻止个人的情感。
10. 注意这里说的是行数，就好像程序的指令数。指令可以跳转产生循环，但是指令数目是有限的。
11. Oron Shagrir，Gödel on Turing on Computability

 

《AI和人》系列快速链接

1. 第1节：经验与逻辑
2. 第2节：公理化的逻辑系统
3. 第3节：图灵机和可计算数
4. 第4节：认知边界上的考量

作者介绍

冯雷(Ray Feng)是Pivotal中国公司MD兼研发中心总经理。Pivotal中国成立至今，冯雷主持了近十亿人民币投资的中国运营和研发体系。作为Pivotal全球产品关键领导人，冯雷为Pivotal公司的数字化理念建立及其对应的Cloud Foundry和Greenplum产品提供战略输入。冯雷于2010年从美国硅谷归国，在美国500强公司EMC旗下组建了Pivotal中国。在归国之前，冯雷居住在美国加州硅谷，在500强企业甲骨文(Oracle)总部从事云计算产品研发。作为云计算最早一批从业人员，冯雷帮助甲骨文云计算资源调度领域成为意见领袖。学术方面，冯雷以浙江省队物理奥林匹克银牌进入北京大学。冯雷在北大实验班（现在的元培项目）接受计算机科学和数学在内的基础学科熏陶，并获得物理学和经济学双学士。冯雷研究生就读于美国匹兹堡市的卡内基梅隆大学并获得硕士学位，在校期间在机器人学院(Robostics Institue)从事教育机器人项目助研。冯雷持有两项美国云计算专利，并著有云计算、大数据和AI的三部曲著作.

 

[如需转载请注明本文URL]
https://digitx.cn/2019/04/19/ai和人_第4节_认知边界上的考量